8-12-2024: The HVAC&R Weekly Edition: Issue #9

We’re laying a foundation so we can develop a better understanding of the relationships we will encounter when using Trigonometry.

To establish a base for the upcoming Advanced Offset formulas we will be learning, we need to review the components of an offset. The placement and description of these components are based on the angle of the offset or the “angle of interest”. Other important observations or questions to ask would be, are the lines entering and leaving the offset parallel or do they form a 90° turn or some other angle?

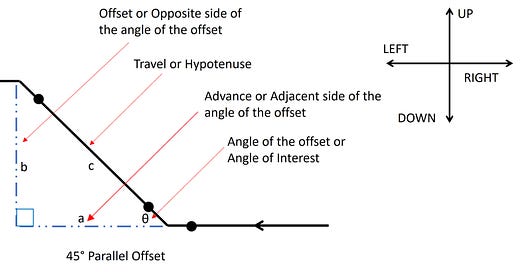
45° PARALLEL OFFSET (Example A)

45° PARALLEL OFFSET (Example A)

Did you notice that each side of the triangle is labeled with two terms? I did that intentionally, the first is the common term used in our industry, the second term is generally associated with the Trigonometric Functions that we will be working with eventually. Looking at the image there are some assumptions we can make regarding this 45° offset based on “The 6 Rules of Right Triangles” (see issue #8). Because the angle of the offset is 45° we know that the offset side and the advanced side of the pipe configuration are equal. That is because both of the interior angles of the offset are equal, based on “The 6 Rules of Right Triangles”. Let’s take a look at the offset when I change the location of the angle of the offset or the “angle of interest”.

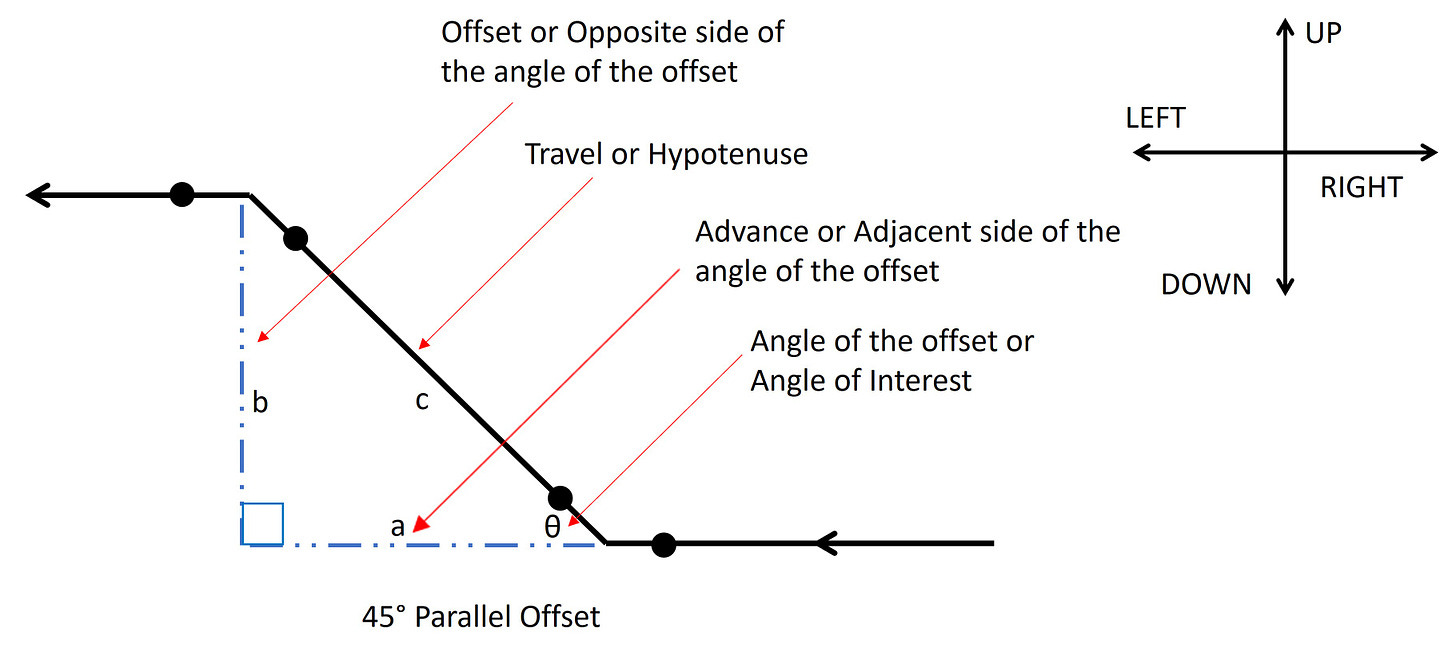
45° PARALLEL OFFSET (Example B)

45° PARALLEL OFFSET (Example B)

Notice how I changed the position of the angle of interest? Its location went from the lower right of the piping configuration to the upper left. The location of the Offset side and Advance side changed as well.

Understanding that becomes much more important with right triangles that do not contain 45° degree angles, and is more note worthy when we begin to study right triangle Trigonometry. What I’m attempting to illustrate is that we are referencing the sides of the triangle created by our offset based on the location of the angle of the offset or the “angle of interest”. Notice how the travel or hypotenuse remained in the same position but the positions of the offset or opposite side and the advance or adjacent side switched. That was because the angle of the offset or the “angle of interest” changed positions.

One or two final observations, the “offset dimension” describes the distance the line was moved or relocated to create a new line running in a parallel path to the original line, while continuing in the same direction. The “advance dimension” describes the distance or space the offset piping configuration takes up in a straight line. Both are described in center to center dimensions. Be careful to describe all dimensions in mixed decimal fractions and record those measurements in center to center fashion, so that all calculated answers will also be in center to center dimensions.

KEY MULTIPLICATION FACTORS FOR 45° OFFSETS:

1. 1.4142

2. .707

3. .4142

The first 2 factors listed above can be applied to any 45° offset configuration to solve for the Travel, Offset, or the Advance side. I will discuss factor #3 when we review equal spread offsets.

45 DEGREE OFFSET FORMULAS:

1. Offset x 1.4142 = Travel

2. Travel x .707 = Offset or Advance

3. The Offset = The Advance

Let me take a brief moment to tell you a little bit about how those 3 Factors came about.

1. 1.4142: It’s probably the first pipe math constant that many of us were introduced to in our pipe trade education. It is actually one of the Trigonometric Functions or Ratios. It compares the Offset or Opposite side to the Travel or Hypotenuse and it’s listed as the Cosecant of a 45° angle. We will explore that a bit deeper as we go along. It is also equal to the √2. I often use the √2 function on my calculator as a quick means to input 1.4142. We use it to find the Travel of a 45° offset when the length of the offset side or opposite side is known.

2. .707: This is another pipe math constant that you may have learned early in your pipe trade education. It too is a Trigonometric Function or Ratio. It represents the Sine or Cosine of a 45° angle. This ratio compares the length of the Offset or Opposite side to the Travel or Hypotenuse of the offset configuration. It also compares the Advance or Adjacent side of a 45 triangle to its Travel or Hypotenuse. Because the side opposite and the side adjacent to the angle of interest are equal in a 45° triangle they share the same Trigonometric function .707. It’s interesting to note that the reciprocal of .707 (1 ÷ .707 = 1.4142) is 1.4142 or the √2. That might spark some interest into the nature of the relationship of the Cosecant to the Sine. We often use .707 to find the length of the Offset or Opposite side and the Advance or Adjacent side of a piping offset when the length of the Travel or Hypotenuse is known.

3. .4142: Although we haven’t formally introduce this little gem yet, it is an important factor when we are working with a series of equally spaced or equally “spread” lines and want to maintain that equal spread though the 45° offset. By now you’ve probably guessed that it too is a Trigonometric Function and is the Ratio for a 22.5° triangle comparing the Offset or Opposite side to the Advance or Adjacent side. It is the Tangent of 22.5° and it allows us to calculate the “Gain” length based on the “Spread” between two or more lines running in parallel. The Tangent is also used to calculate the “takeoff” of an odd angle weld fitting.

Here are a couple of practical examples of 45° offsets that use these factors lets set if you can figure out the required dimensions.

FINDING THE TRAVEL

USING 1.4142 TO SOLVE FOR THE TRAVEL DIMENSION:

For most of us this is probably quite rudimentary to solve, here are the key steps.

• Convert the mixed rational fraction to a mixed decimal fraction 27 ⅜” c₂c 3 ÷ 8 = .375→ 27.375”

• Multiply the offset dimension by 1.4142: 27.375 x 1.4142 = 38.714”

• Convert the decimal fraction to a rational fraction in 16ths: .714 x 16 = 11.4→ 11

• Rewrite the final answer as a mixed fraction: 38-11/16” c₂c 

FINDING THE OFFSET OR ADVANCE:

USING .707 TO SOLVE FOR THE OFFSET DIMENSION:

• Multiply the travel dimension by .707: 47.875 x .707 = 33.8476”

• Convert the decimal fraction to a rational fraction in 16ths : .8476 x 16 = 13.5 → 14/16 → ⅞”

• Rewrite the final answer as mixed rational fraction: 33-⅞”c₂c

• The offset dimension and the advance dimension would be the same length.

FINDING THE TAKEOFF FOR 45° AND 90° WELD FITTINGS:

FINDING THE TAKEOFF FOR 45° AND 90° WELD FITTINGS:

It’s important to know the makeup or takeoff when working with any fitting, with copper and threaded pipe it is usually a quick measurement to find that dimension. With weld fittings, the takeoff for a “standard” radius 45° and 90° fittings has been standardized throughout the industry. When finding the takeoff for a 45° fitting I use the “Half, Half, Half Method”. Beginning with the nominal pipe size of your fitting Half it, then Half it again and Half it one final time. You will then add the second and last numbers of that sequence to get the takeoff for a 45° fitting. Remember there are two 45° fittings in most travel pieces, so the takeoff must be subtracted from the center to center dimension of the Travel twice.

For weld 90° fittings we would use the nominal pipe size and take half of that number and add it back to the nominal size. Essentially it’s multiplying it x 1.5. Both these methods work for pipe sizes from 2.5” through 48”.

45 EQUAL SPREAD OFFSETS AND USING .4142 TO FIND THE GAIN:

The description, “Equal Spread Offset” is deceiving in that it implies that all lines in an equal spread offset must be equally spaced to one another. That is not the case. It simply means that any two lines must be equally spaced throughout the offset, but the spread can vary from line to line. Here is an example.

SOLVING FOR A 45° EQUAL SPREAD OFFSET:

Here is our problem, we have four lines that are equally spaced. The first three lines have a 6” spread between A and B, the fourth line has a spread of 10” (Line C) from its neighbor. In this type of configuration I like to start by solving for the Travel dimensions, then work the left side first, solving for the Gains for each line, then apply that to the right side. In this case the right side “Gains” are actually “Losses” moving from bottom to top. One unique characteristic about a 45° Parallel Equal Spread Offset is that all the Travel dimensions (T₁ - T₄) are the same length center to center regardless of the spreads or the pipe size, and that there will always be Gains on one side and Losses on the other side. Remember that Gains are the distance a line must extend past the neighboring 45° fitting to maintain the equal spread. So let’s do it!

SOLVING FOR A 45° EQUAL SPREAD OFFSET:

• The Offset x 1.4142 = Travel

• Solving for the Travel (T₁ - T₄): 57” x 1.4141 = 80.610” Travel

• .610 x 16 = 9.76 → 10/16 → 80 ⅝”c₂c Travel for all four lines.

• The Gain = Spread x .4142

• Solving for the Gain for the 6” spreads: 6” x .4142 = 2.4852” Gain

• .4852 x 16 = 7.7→ 8/16→ 2-1/2” This is the Right side “Gain” and Left side “Loss” for lines A, B, D and E.

• Solving for the Gain for the 10” spread: 10” x .4142 = 4.142” Gain

• .142” x 16 = 2.2→ 2/16 → 4 ⅛” This is the Gain and Loss for line C and F.

We now have all the dimensions we need. It’s just a matter of adding the Gains and subtracting the Losses to find the dimensions of lines A, B, C, D, and F. We also have dimensions for the Travel pieces for (T₁ - T₄).

• We determined T₁ - T₄ are all 80 ⅝”c₂c

• Line A =24” plus the Gain→ 24”+ 2 ¹/₂” = 26¹/₂” e₂c

• Line B plus the Gain→ 26¹/₂” + 2 ¹/₂” = 29”e₂c

• Line C plus the Gain→ 29” + 4 ⅛” = 33 ⅛”e₂c

• Line D= 60”minus the Loss 60”- 2 ¹/₂” = 57¹/₂”c₂e

• Line E minus the Loss→ 57¹/₂”- 2 ¹/₂” = 55”c₂e

• Line F minus the Loss→ 55” - 4 ⅛” = 50 ⅞”c₂e

That is how it’s done, but you have some home work! Figure out the takeoff for the 3” and 4” 45° fittings. Then determine the end to end cut dimension for the Travel lengths and calculate the lengths for Lines A-F.

Next week we put on our Togas, play a little game of Pythagorean Theorem, as I serve up some PI with a side of Radian pudding. And we finish it off with a portion of Trigonometry. Thanks for your patience as we move toward our final goal.

I appreciate your feed back so please leave a comment, or if you have any questions please feel free to reach out. If you know someone that may find this kind of information helpful please feel free to share.

Be safe and have a good week.

(See previous issue.)