8-19-2024: The HVAC&R Weekly Edition: Issue #10
Simplistic in design, elegant in structure, they act as Sentries to a realm of discovery. Sine, Cosine, and Tangent stand poised to reveal their secrets, just say the magic words. "SOH-CAH-TOA"
Here are the answers from last weeks 45° Equal Spread Offset Session. How did you do?
The 3” 45° fittings have a takeoff of 1⅞”.
The 4” 45° fittings have a takeoff of 2 ¹/₂”
We determined T₁ - T₄ are all 80 ⅝”c₂c: So T₁ - T₃ = 80 ⅝ - (1⅞ + 1⅞) = 76 ⅞ e₂e; T₄ = 80 ⅝” - (2 ¹/₂”+ 2 ¹/₂”) = 75 ⅝”e₂e
The Left Base Line = 24”e₂c; 24” - 1⅞”= 22 ⅛ “e₂e
Line A= 24” plus the Gain→ 24”+ 2 ¹/₂” = 26¹/₂”e₂c; Line A= 26¹/₂”- 1⅞” = 24⅝” e₂e
Line B plus the Gain→ 26¹/₂” + 2 ¹/₂” = 29”e₂c; Line B = 29”- 1⅞”= 26¹/₂”e₂e
Line C plus the Gain→ 29” + 4 ⅛” = 33 ⅛”e₂c; Line C = 33 ⅛”- 2 ¹/₂”= 30 ⅝” e₂e
The Right Base Line = 60”e₂c; 60” - 1⅞”= 58 ⅛”e₂e
Line D = 60” minus the Loss→60”-2 ¹/₂” = 57¹/₂”c₂e; 57¹/₂” - 1⅞”= 55 ⅝” e₂e
Line E minus the Loss→ 57¹/₂”- 2 ¹/₂” = 55”c₂e; 55”- 1⅞”= 53 ⅛”e₂e
Line F minus the Loss→ 55” - 4 ⅛” = 50 ⅞”c₂e; 50 ⅞”- 2 ¹/₂”= 48 ⅜” e₂e
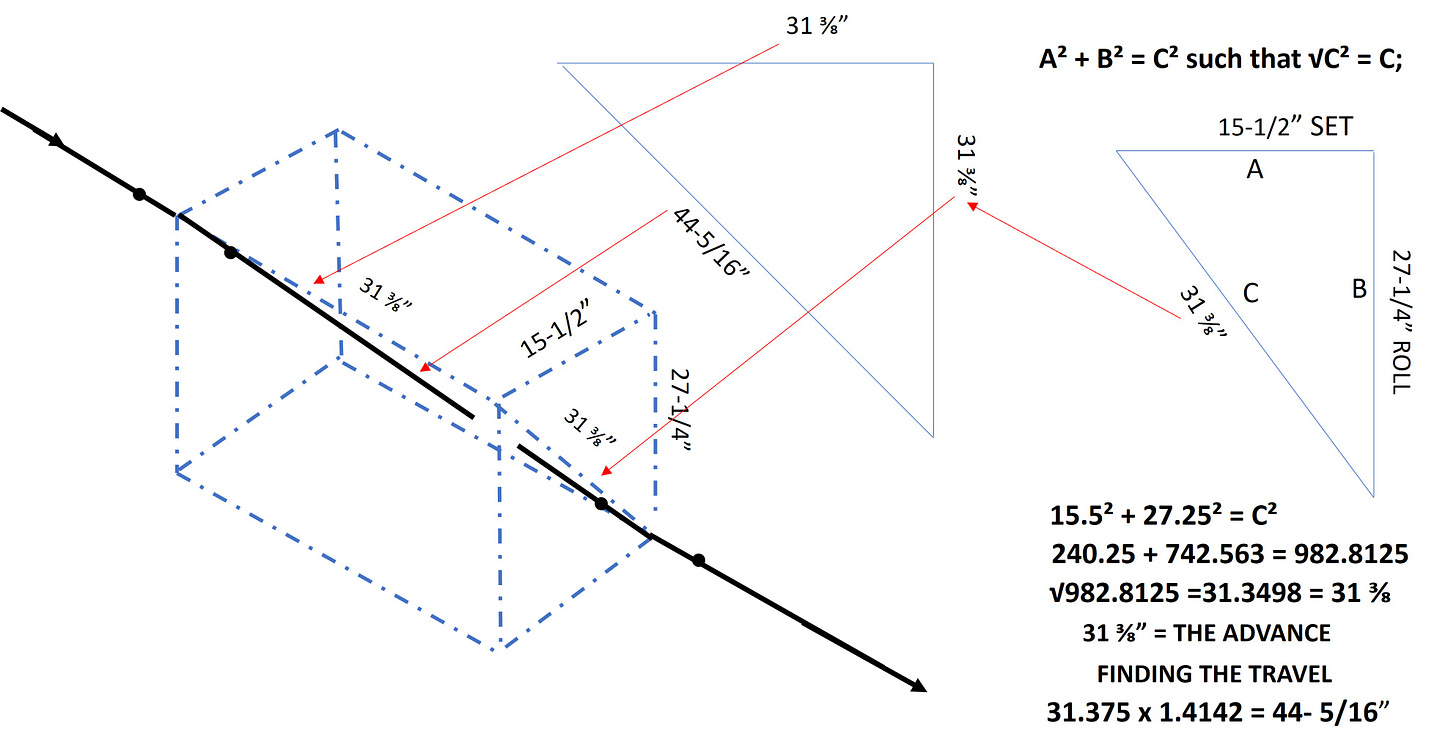
To finish our review of 45° offsets we need to tackle the 45° Rolling Offset. The word “tackle” might give the impression it’s a difficult offset to solve, and prior to handheld calculators and Smartphones that would be a pretty fair statement. However with today's technology it’s a piece of cake. The 45°Rolling Offset solution involves using The Pythagorean Theorem. The mere mention of it brings back memories, as I catch myself mentally reciting the Theorem in my head like a Nerdy Nursery Rhyme. Pythagorean Theorem: A² + B² = C² such that √C² = C.
THE PYTHAGOREANS
They were a Mystic group of scholars lead by the Greek philosopher Pythagoras. They believed that the study of mathematics and numbers were sacred and treasured them for their beauty rather than using them for any practical purpose. They never met in groups greater than ten because they felt ten was the perfect number. Rumor has it, they formed the first bowling league and called themselves Team Tetractys.
Pythagoras was credited with developing The Pythagorean Theorem, which said; if the length of one side of a right triangle is squared, and added to the squared length of the other side of a right triangle, their sum will equal the square of the hypotenuse. By taking the square root of the sum of the two sides, it will be equal to the length of the hypotenuse. You gotta’ hand it to those Pythagorean’s, when you form a secret club it’s best to come up with a good sacred creed.
The familiar 3-4-5 triangle is used by many craftspersons across many different trade associations to layout a 90° right triangle. It is an example of the practical usage of The Pythagorean Theorem. That ratio of 3-4-5 can be used with any similar triangle to layout a 90° right triangle of that proportion, such that a 38 ⅞”; 51-13/16”; 64-5/16” triangle would also produce a 90° right triangle. Some wrongly assume that a 3-4-5 triangle is representative of a 30° x 60° x 90° triangle which is false, and we can prove that together when we dive into the Trigonometric Functions.
SOLVING A 45° ROLLING OFFSET:
A 45°rolling offset lets the pipefitter change both elevation and direction at the same time using a 45°offset that transects both the horizontal plan and the vertical plane using two 45°fittings. With out that configuration it would require three 90° fittings. It becomes even more advantageous when one of those dimensions is less than the takeoff of two 90° fittings. Here is one method to solve that problem.
THE 45° ROLLING OFFSET:
THE 45° ROLLING OFFSET:
The solution for this offset is found by using Pythagorean’s Theorem and applying it to the “Set-A” 15-1/2” and the “Roll-B” 27-1/4” to find “C”. The terms “A” and “B” are interchangeable, meaning swapping the “Set-A” label for the “Roll-B” label does not affect the answer. Dimension “C” becomes the Offset as well as Advance of the traversing offset configuration and it can be multiplied by 1.4142 to find the “Travel” center to center. Essentially what we’ve done is we’ve taken a 45°offset that cut through two separate planes and isolated it into one single plane.
I have coined a term I call The Perfect 45° Rolling Offset. It comes into play when the Roll and the Set are the same dimension. The Travel can be found by doubling either of the two dimensions. Mathematically it’s accurate and sound, with no exceptions unlike some of the short cuts we see in our trade. It can come in handy when either the Roll the Set distance is critical to miss an obstacle and the other dimension is not. I think Pythagoras would have loved the simplicity of it!
THE SENTRIES TO THE REALM OF SINE, COSINE, AND TANGENT
SPEAK SOH-CAH-TOA AND ENTER
As a struggling math student in high school, I couldn’t seem to understand how these “Trig. Functions” were created. Just where in the hell did these numbers come from? In those days, in the back appendix of our Trig. text books, there were column upon column of ciphered numbers. Taken to 7 decimal places, indexing angles from 0° to 90°, each column was listed under the heading of Sine, Cosine, Tangent, Cosecant Secant, and Cotangent. Even describing it today makes me breakout in a sweat, causes my pulse to race, and respirations to quicken. Stress is an ugly thing.
At the end of one particular class session I asked the instructor, “How do they get these numbers?” He went on about derivations of some sort, drawing circles and curvy lines on the chalk board, it resembled something from a bad science fiction movie less the Tesla coil. It was torture. It was a semester ending in a D⁺. And that was being nice, because he really didn’t want to see me in his class next semester.
I just needed one word, RATIO! That was my light bulb moment to unlocking the mysteries of Trigonometric Functions. They are Ratios comparing one side of a triangle to one of the other two sides. The pneumonic SOH-CAH-TOA is an easy way to recall the order of those ratios for the Sine, Cosine, and Tangent. If I had only known. Sound familiar? Don’t despair brothers and sisters I’m here to help.
THE SINE Sine θ = OPPPOSITE ÷ HYPOTENUSE
The first ratio to examine is called the Sine. The Sine of an angle compares the opposite side of a triangle to the hypotenuse. This is done by dividing the length of the opposite side by the hypotenuse as referenced from the “angle of interest”. This ratio begins at a value of zero for an angle of 0° (degrees) or a horizontal line, and increase as the angle increases to a ratio value of 1 at 90° or a vertical line. The ratio of the Sine is commonly used to solve piping problems that involve the offset and the travel. It is also be used for locating the centerline point when laying out a mitered weld-fitting. To convert the ratio to degrees and decimal degrees you must use the Arc-Sine⁻ ¹ (2nd function on the calculator).
THE SINE SOH Sin θ = OPPPOSITE ÷ HYPOTENUSE
THE COSINE Cosine θ = ADJACENT ÷ HYPOTENUSE
The Cosine of an angle is comparing the adjacent side of a triangle to its hypotenuse. This is done by dividing the adjacent side by the length of the hypotenuse as referenced from the “angle of interest”. This ratio begins at a value of 1 for a 0°(degree) angle or a horizontal line and decreases to a zero value for a 90° angle. The ratio of the Cosine can be used for locating the centerline point when laying out a mitered weld-fitting. To convert the ratio to degrees and decimal degrees you must use the Arc-Cosine⁻ ¹ (2nd function on the calculator).
THE COSINE CAH Cos θ = ADJACENT ÷ HYPOTENUSE
THE TANGENT Tangent θ = OPPOSITE ÷ ADJACENT
Of the three primary Trigonometric Functions the Tangent is the only one that has a ratio that does not use the hypotenuse. The Tangent compares the opposite side of a triangle to the adjacent. This is done by dividing the opposite side by the length of the adjacent side as referenced from the “angle of interest”. This ratio starts a zero at 0° (degrees) and increases to infinity as it approaches 90° and then becomes undefined at 90°. The ratio of the tangent is used when calculating the gain for an equal spread offset, and can be used to find the take-off of mitered weld-fittings. To convert the ratio to degrees and decimal degrees you must use the Arc-Tangent⁻ ¹ (2nd function on the calculator).
THE TANGENT TOA Tan θ = OPPOSITE ÷ ADJACENT
THEIR RECIPROCALS
We were just introduced to the three primary Trigonometric Functions Sine, Cosine, and Tangent. There are in fact three additional Trigonometric Functions which are reciprocals of the primary ratios. Those are Cosecant, Secant, Cotangent.
THE COSECANT Csc θ = HYPOTENUSE ÷ OPPOSITE
This is the ratio that a pipefitter might use to calculate the travel of a 45° offset, 1.4142 is the ratio that compares the hypotenuse of a 45° offset configuration to the opposite or offset side, as referenced from the “angle of interest”. It is the reciprocal of the Sine. It’s interesting to note that the reciprocal of 1.4142 is .707. I think the tradesman favored a factor they could multiply with rather than to be faced with a division problem involving a decimal. Think about it, they only had pencil and paper for math calculations; Smartphones and hand held calculators hadn’t been invented yet, nor had Star Trek, or Captain Kirk! We can access the Cosecant function on a scientific calculator by taking the Sine of the desired angle and use the 1/x key to find the Cosecant of the angle.
THE SECANT Sec θ = HYPOTENUSE ÷ ADJACENT
The Secant is defined as the hypotenuse of a triangle divided by the adjacent side of the triangle, as referenced from the “angle of interest”. It is the reciprocal of the Cosine. We can access the Secant function on a scientific calculator by taking the Cosine of the desired angle and use the 1/x key to find the Secant of the angle.
THE COTANGENT Cot θ = ADJACENT ÷ OPPOSITE
The Cotangent is defined as the adjacent side of a triangle divided by the opposite side of the triangle, as referenced from the “angle of interest”. It is the reciprocal of the Tangent. We can access the Cotangent function on a scientific calculator by taking the Tangent of the desired angle and use the 1/x key to find the Cotangent of the angle.
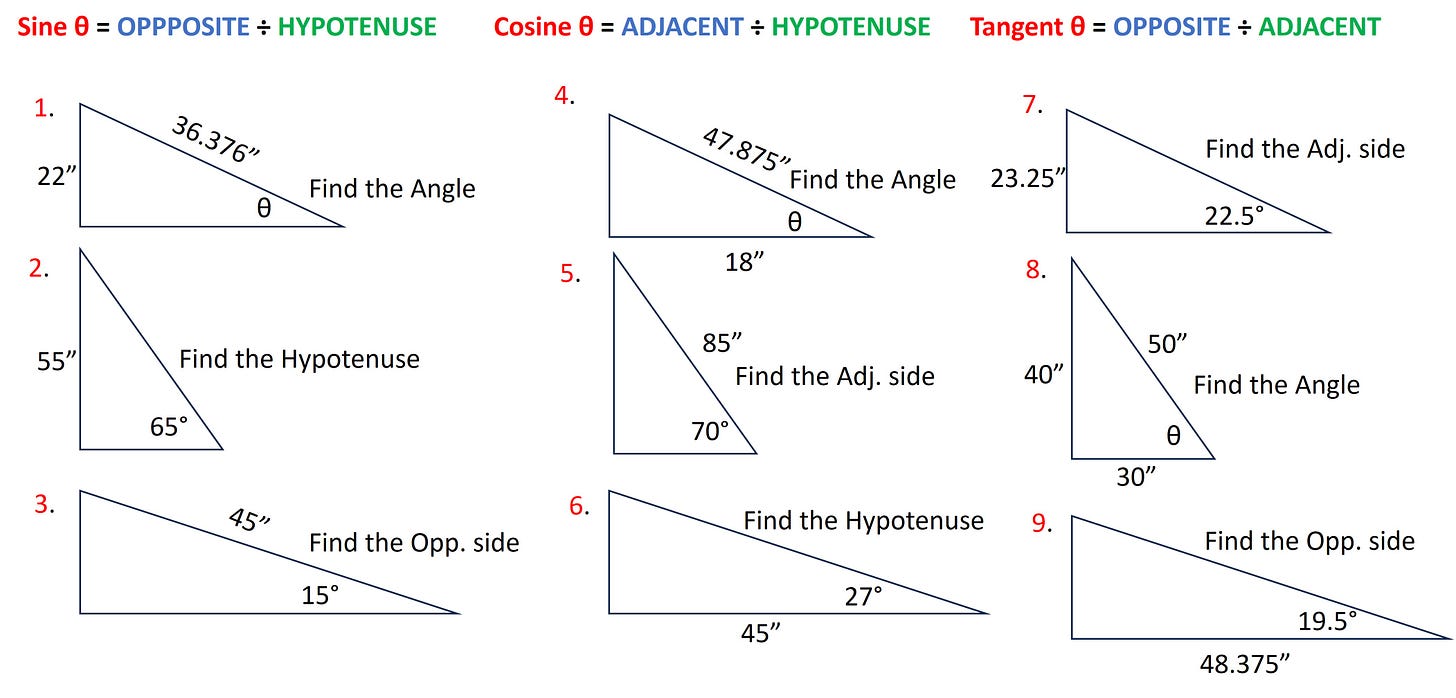
EXERCISES USING VARIOUS TRIGONOMETRIC FUNCTIONS:
EXERCISES USING VARIOUS TRIGONOMETRIC FUNCTIONS:
I’m going to leave things off here with some practice exercises for you to attempt. Try your hand at these, use the 3 examples provided earlier in this session if you get stuck. Don’t worry, I’ll review these next week and then we will go over some techniques we can use to miter a weld bend 90° fitting into our desired angle.
I do appreciate your feed back so please leave a comment, or if you have any questions please feel free to reach out. If you know someone that may find this kind of information helpful please feel free to share.
Be safe and have a good week.