9-2-2024: The HVAC&R Weekly Edition: Issue #12
Diamonds can come Square Cut or Emerald Cut, Heart Shaped or Pear Shaped, But according to my old friend Dave, π are only round.
Pi (π) ARE ROUND
There was a pipefitter I had known for years who would always greet me with the same simple math query every time we saw each other. He would always say, “A.J. what’s the formula for the area of a circle”? My reflexive response was always, “Dave, π R².” He’d crack a small grin, wag his finger and shake his head and say, “Silly Boy, Pie are Round.” I know it’s sophomoric, even childish, but I truly miss this man’s gentle spirit and hearing his silly little math pun regarding this renowned irrational number.
THE CIRCUMFERENCE OF A CIRCLE
The relationship of Pi (π) to a circle, to its circumference, and to its radius are all interlocked and crucial in our exploration of Trigonometry and many of our Advanced Offset techniques. More to the point it’s important in the development of the skill sets we need to layout odd angle mitered fittings from standard 90° weld bend fittings.
First understand that π describes the ratio of the circumference of a circle to its diameter. That means the circumference is ≈ 3.1415 times greater than the length of the diameter of a circle regardless of the size of the circle.
Pi (π) And The Circle:
Pi (π) and The Circle:
There are several different techniques that are being taught to both apprentices and journey-persons in our trade to layout angles and to scribe weld bend mitered fittings. I’ve seen everything from framing squares, to protractor compasses, to a string or chain 57-1/4” long.
I would prefer to use a scientific calculator, a tape measure and a framing square or tri-square to layout my mitered fittings. To do that we need to understand what a Radian is.
THE RADIAN
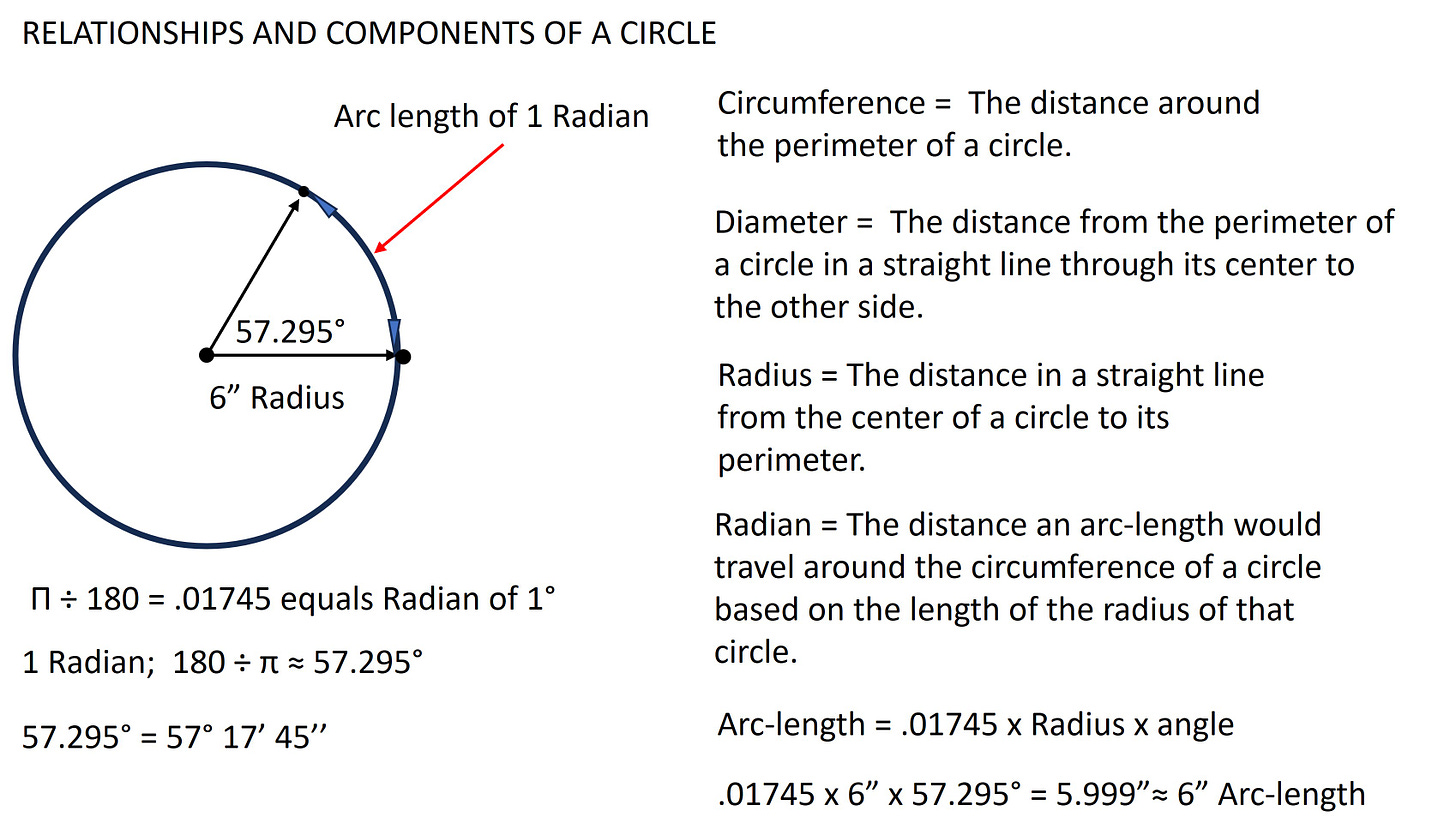
A radian is a unit of angular measure, just like degrees, or gradients. As a matter of fact π can be used as a unit of angular measure as well. Each has its own purpose. In simple terms a Radian is the distance an arc-length would travel around the circumference of a circle based on the length of the radius of that circle. Sounds like a word salad doesn’t it. Let’s see what that looks like.
THE RADIAN AND THE UNIT CIRCLE.
THE RADIAN AND THE UNIT CIRCLE
The fact 1 Radian is equal to about 57.2957° explains why the Chain Method for fitting layout with it’s 57-1/4” String or Chain works. In those proportions, an angle of 1° would represent an arc-length of 1 inch on the circumference of a circle with a radius of 57-1/4” inches. I feel if you choose to use an alternative method in seeking a solution, like the Chain Method, it’s best to understand why or how that method works.
USING THE RADIAN AND TRIGONOMETRY FOR FITTING LAYOUT
All standard long radius 90° weld fittings are manufactured under a specification that requires the radius of the fitting is to be drawn through a mandrill or die that is 1.5 times the nominal pipe size. Using that information and the wall thickness of the pipe we can calculate the Outside radius and the Inside radius for any weld fitting from 2” to 48”.
(Pg. 26 lists 90° fitting data; Pgs. 130, 139-143 lists wall thickness data)
RADIANS AN ANGLES AND RADII! OH MY!
Here are several tutorial slides that show how we put it all together so we can accurately layout any mitered fitting from a 90° weld-fitting.
ARC LENGTH LAY-OUT
ARC LENGTH LAY-OUT
Here is how we lay out and mark the Outside and Inside Arc-lengths at the Heel and Throat of the fitting using the information we’ve presented so far. Make sure you mark the fitting you intend to keep with an X. When the desired angle is close to 45°, with only three or four degrees difference one way or the other it’s easy to grab the wrong fitting. It’s not so easy to make that wrong fitting work.
This technique can also be used to find an intersection point on pipe headers when a threadolet, weldolet, or pipe saddle might need to be placed at a specific angle. Use your imagination! .
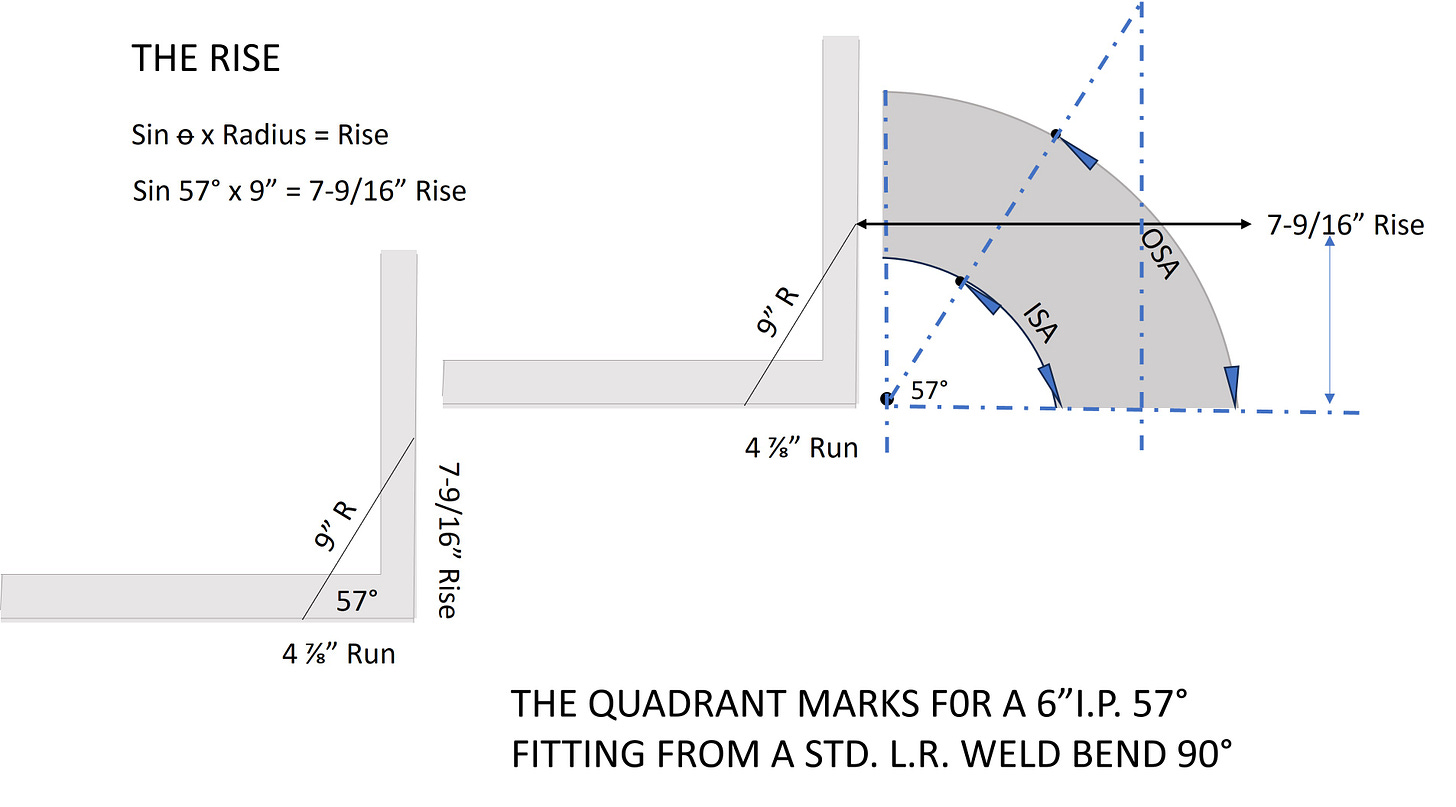
MARKING THE TWO SIDE QUADRANTS (The Rise)
MARKING THE TWO SIDE QUADRANTS (The Rise)
Using a framing square I lay out a 57°triangle using a hypotenuse equal to the center line radius of the fitting and the Sine of the angle to find the opposite or rise side of the triangle. This produces a reference mark that is dead on center of the fitting at the angle we will be cutting. Scribe a mark on both the left and right sides of the fitting. Then flip the fitting around.
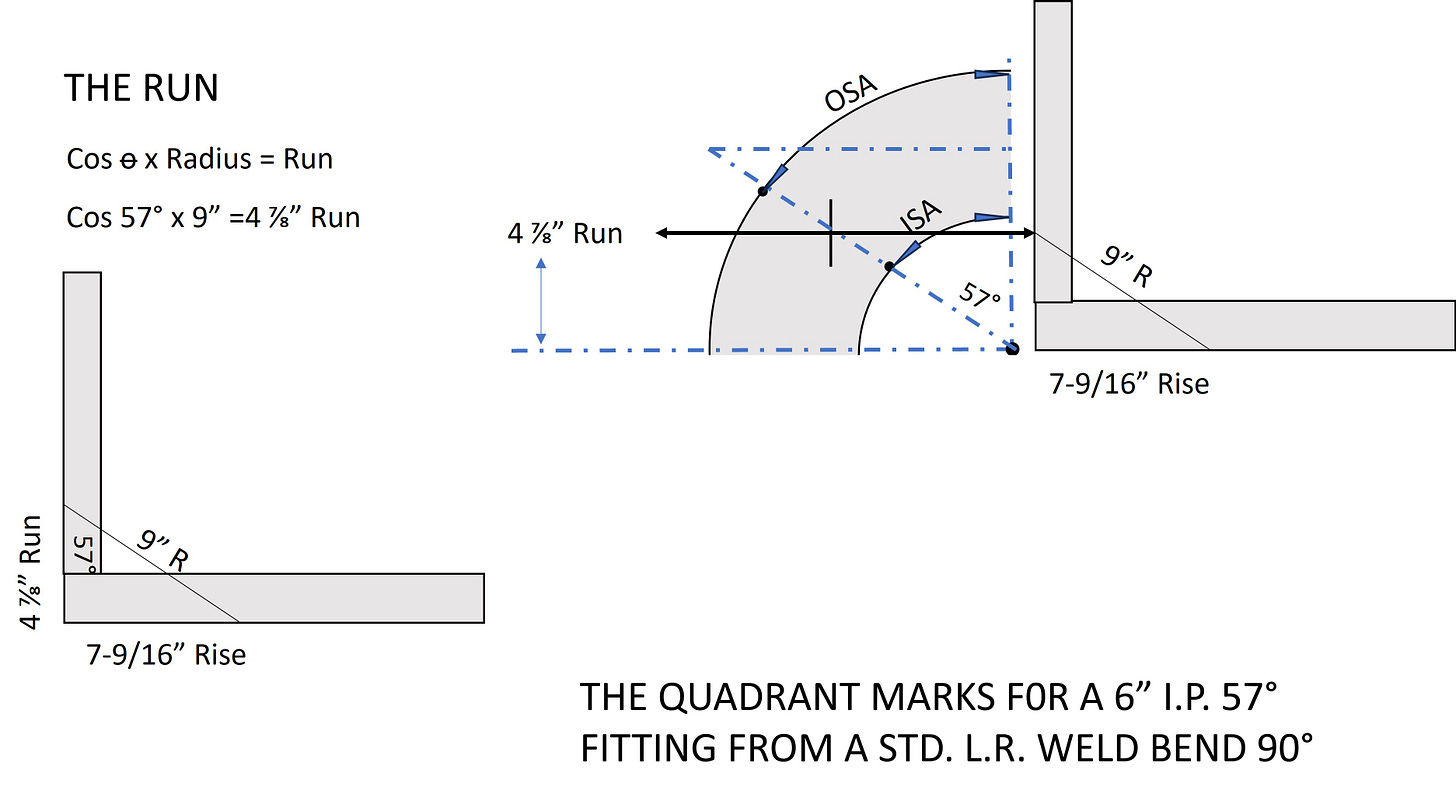
MARKING THE TWO SIDE QUADRANTS (The Run)
MARKING THE TWO SIDE QUADRANTS (The Run)
Once you’ve flipped the fitting over layout the same 57° triangle but this time use the Cosine and the same 57°angle to find the adjacent or run side of the triangle and mark both sides of the fitting. You should have four points, dividing the fitting into four equal quadrants representing a 57°fitting.
You can use a small 6’ flexible tape measure (I use a piece of braided masons line) to connect all four points and with a sharpened soapstone or pipe marker. I like to center punch my line once I’ve marked it to protect the line. This can now be cut with a Port-a-band then beveled. If the fitting is too big for a Port-a-band then cut it with an oxy-acetylene torch but, DO NOT ATTEMPT TO BEVEL CUT. If you do it will make the fitting the wrong angle, torch cut it straight then face it up with a side grinder and then bevel it, or you can back bevel it with a torch.
I’m often asked if I’m concerned with the weld gap fit-up causing a dimensional problem, especially for a direct fitting to fitting type offset. The answer is no not really, I’ve done the math and because the gap-rod (3/32”) is in the travel of the offset and the fitting is being straight cut from a 90°weld bend it has little measurable impact on the overall offset dimension. For offsets ranging from a 10°offset angle up to an 80°offset angle, it adds as little as 1/64” at 10° up to 1/16” at 80°to the overall offset dimension.
IT’S YOUR TURN
I would like you to try to layout a mitered fitting from a 10” 90° weld bend. You can look up the wall thickness in the attached reference manual or trust me when I say the O.D. of 10” Iron Pipe is 10.750”. Let’s make it interesting and layout a 38°mitered fitting. Find the following:
Find the center line Radius (takeoff) for a 10” 90° weld bend
Find the OSA→ (Outside Arc-Length) for a 38° mitered from a 90°
Find the ISA→ (Inside Arc-Length) for a 38° mitered from a 90°
Find the Rise dimension for the Quadrant Marks for 38°
Find the Run dimension for the Quadrant Marks for 38°
CHALLENGE! Find the takeoff face to center for that 38°fitting. (Hint, it requires using the Tangent).
When we regroup next week I will provide the answers, show you how to find the take-off face to center, and eventually show you how to accurately fit that to a piece of pipe using a two foot level and framing square. But not before we move onto five Advanced Offset Formulas.
Until then I do appreciate your feed back so please leave a comment, or if you have any questions please feel free to reach out. If you know someone that may find this kind of information helpful please feel free to share.
Be safe and have a good week.