8-26-2024: The HVAC&R Weekly Edition: Issue #11
Cleaning up some unfinished business before moving on. This short post is specific to last weeks exercise.
Last week I assigned some homework that involved using what we had learned about right triangles and Trigonometric Functions. There were 9 problems that involved using the 3 Primary Trig. Functions: Sine, Cosine and the Tangent. This Issue is specifically written to provide those solutions. Remember?
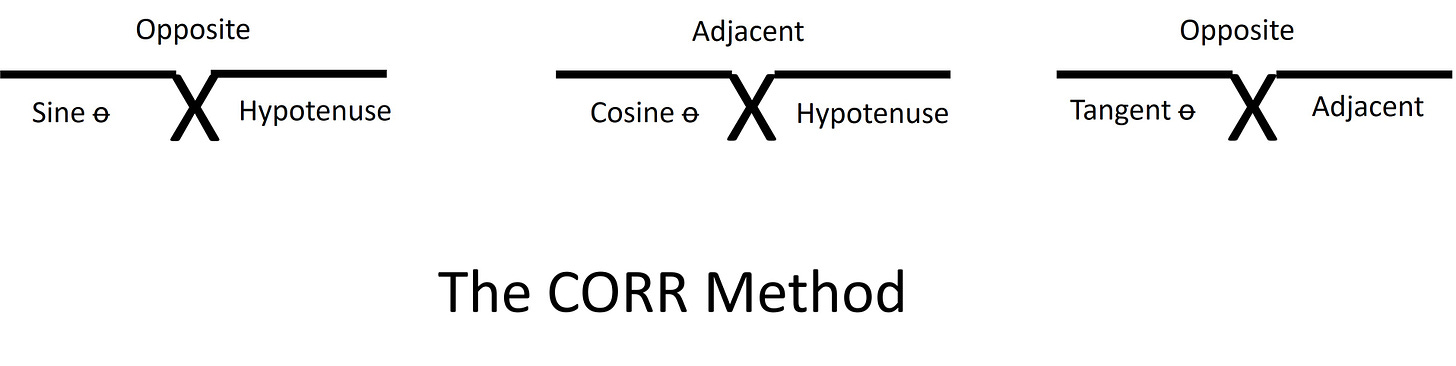
Some of us may be a bit Algebraically challenged and find that manipulating an equation to solve for an unknown value unfamiliar, I’ve been there and struggled with that too, so I’ve put this tool together to help you. The CORR Method works on any two factor equation written in the form of A x B = C
THE CORR METHOD FOR SOH-CAH-TOA FOR SINE, COSINE, AND TANGENT
This will allow you to enter the data and solve for the unknown value without having to manipulate the equation. If the two known terms are on either side of the X they must be multiplied to find the third. If one of the known terms is above the X then the lower known term must be divided into the upper known term. All angles must be converted to their respective Trigonometric function before solving. Any answer resulting in a Trigonometric function can be converted to an angle by accessing the Sin⁻¹, Cos⁻¹ and Tan⁻¹ using the 2nd key on your calculator. Seriously, who carries a Trigonometric Function table in their pocket any more!
If you have a DD (Decimal Degrees) > DMS (Degrees Minutes Seconds) function key on your calculator you can access that with the 2nd function and switch from Decimal Degrees to Degrees Minutes Seconds and back. Although for all of my calculations I leave the terms in DD as I rarely have a need to express the angle in Degrees Minutes and Seconds, it would be more for fun.
If you want it in those terms but don’t have a DD to DMS function on your calculator then do this; separate the whole Degrees from the decimal and multiply the decimal by 60 (that will be minutes and decimal minutes). Next separate the whole minutes from the decimal and multiply the decimal by 60 (that will be seconds). If the decimal seconds portion is 5 or greater round up to the next second. Like I said it’s for fun, I usually leave them in DD
YOUR NINE PROBLEMS:
FINDING THE SOULTIONS:
Sin θ = 22” ÷ 36.376”; Sin θ = .60479; Sin⁻¹ = 37.214°= 37°12’ 50’’
55” ÷ 65°Sin = 60.685” = The Hypotenuse
15°Sin x 45” = 11.646”= The Opposite Side
Cos θ = 18” ÷ 47.875”; Cos θ = .37597; Cos⁻¹ = 67.9151°= 67°54’ 54’’
85” x 70°Cos = 29.071”= The Adjacent Side
45” ÷ 27°Cos = 50.504”= The Hypotenuse
23.25”÷ 22.5°Tan = 56.130”= The Adjacent Side
Tan θ = 40”÷ 30”; Tan θ = 1.33333; Tan⁻¹ = **53.1301°= 53°7’ 48’’
48.375 x 19.5°Tan = 14.329”= The Opposite Side
Do you recall our earlier discussion regarding The Pythagorean Theorem and 3-4-5 triangles? In that Session I mentioned that some folks wrongly assumed that a 3-4-5 triangle was representative of a 30° x 60° x 90° triangle. **Problem #8 is proportionally similar to a 3-4-5 triangle with its two acute angles of 36.87°and 53.13° forming the right triangle. That addresses the 3-4-5, vs. 30°x 60°x 90° triangle myth and proves it’s a fallacy or fantasy depending how it moves you.
Next week come gather round, and I’ll tell you a little story about a circle.
I do appreciate your feed back so please leave a comment, or if you have any questions please feel free to reach out. If you know someone that may find this kind of information helpful please feel free to share.
Be safe and have a good week.